Imtakt Tswett

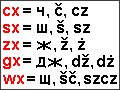
Delame...

ORBITAL SYMMETRY FORCE AS A FORCE OF THE CLASSICAL FORCE FIELD
(WORK IN PROGRESS....)
Svetlana Sinodinou

Post-graduate student, Faculty of Chemistry, University of Belgrade, present adress of the author : D.Areopagitou 2, 60100 Katerini, Greece
e-mail: sinko13@hol.gr

Abstract

Orbital symmetry can influence MO energies and a conformational path of some reactions, so it can be treated as separate force, ie. barrier, the orbital symmetry barrier, Vos. It' s place in the classical Force Field is based on two induced approximations, which distribute the classical FF on one more force and associate certain values to it. Also, a prediction of Vos is made by using the Group Theory.

Key words: Orbital symmetry, Transition operator, FF.

Introduction

In the classical Force Field (FF) approach the total conformational ("strain") energy Vt is calculated as a sum of individual potential energy contributions[1]:

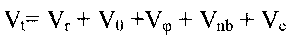
(equation 1)

where Vr is bond strain (energy of the bond length oscillations), Vè is Beyer's (or bond angle ) strain, Vö is Pitzer's (or torsional) strain, Vnb is (attractive and repulsive) non-bonded strain, and Vc is a nonbonded interaction caused by an unequal distribution of charges in the molecule (Coulomb interaction).
In rare cases, the orbital symmetry might influence the most simple conformational path, enlarging the torsional strain or forbidding the reaction [2] of a conformational change. In most cases, it allows the classically predicted conformational path and thus remains unnoticed.
Also, conformational changes influenced by OS in most cases occur in short - living excited states . This is another reason why it was not treated by the classical FF. However, knowledge of the exact conformation in the excited state enables other possibilities, such as stereospecific reactions etc.
Since the classical FF doesn't include this force as a distinct force, it can not explain the symmetrically forbidden conformational path. However, if the path is permitted, the contribution of Vos is included in other empirical parameters of the eq. (1).
The effects of orbital symmetry on the conformational path of concerted reactions were explained at 1965. [2],[3]. They were incorporated into the coming up computer chemistry calculations, but not considered in the classical FF. The increasing need in taking in account the Vos in the conformational calculation, from one side, and simplicity of prediction of Vos in many cases, from the other, enable the induction of Vos in the classical FF.

Approximation of the Orbital Symmetry Strain, VOS


Vos either permits the classically predicted conformational path or forbids it. In the first case, Vos = 0,0 kJ/mol. In the second case,
Vos= +? or Vos >> V t. Equation (1) could be transformed as :

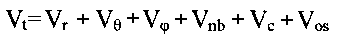
(equation 2)

Vos can be obtained as an activation energy, Eact, for example as an energy increase in MO energy, or electron transition energy, needed for a thermal or photochemical conformational reaction. The other strains, Vr , Vè ,Vö , Vnb and Vc are also obtained using IR, Raman, UV and other spectra.
Since Vos in this approximation has only two values, 0 or ?, i.e. if the reaction is symmetrically either permitted or forbidden, a certain value doesn't need to be associated to Eact.



Approximation of the Orbital Symmetry Strain value, Vos


Vos in a symmetrically permitted conformational path, if not equal to 0 or ?, is equal to the measured value of an observable.
In some cases, a certain value could be associated to Vos as a difference in energy . A system absorbs the energy which has known and measurable value. For example, an electron transition from HOMO to LUMO needed to permit symmetrically a torsion . A measured value of an electron transition should be put as Vos .

Prediction of Vos according to the Group Theory


An electron transition is permitted if the transition momentum is different from zero [4]:

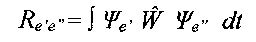
(equation 3)

i.e., if the product of wavefunctions of the initial and the final state Øe' Øe" has the same symmetry as a dipole momentum operator W . The components of the dipole momentum operator Wx, Wy and Wz have the symmetries A' , A' and A", respectively, in the Cs point group. The initial and final states have A' and A" symmetries. The transitions are:

along x and y axes: A' x A' x A" = A" => forbidden
along z axis: A' x A' x A" = A' => permitted.

If an electron transition from the chosen initial state, needed to permit a symmetrically forbidden conformational path from this initial state, is forbidden , according to this examination, than Vos = ?.


References

[1] Niketic, S.R.: Rasmussen, K. The Consistent Force Field, Springer-
Verlag, Berlin-Heidelberg-New York, 1987.

[2] Morrison, H.T.; Boyd, R.H. Organic Chemistry, Allyn and Bacon, Inc.,
Boston, Massachusetts, 1973.

[3] Hoffmann, R. J. Chem. Phys., 1963, 39, 1397.

[4] Herzberg, G. The spectra and Structure of Simple Free Radicals:
An Introduction to Molecular Spectroscopy, Cornell University Press,
Ithaca, New York, 1985.

Acknowledgments:
The author would like to thank Professor S.R. Niketic for guidance and support. The Ministry of Science and Technology of the Republic of Serbia is Thanked for a financial support.

WORK IN PROGRESS...

Delame...